문제

공개키 알고리즘 중 Rivest, Shamir, Adleman에 의해 설계된 RSA 알고리즘을 구현하라

로직

1. 2개의 소수 (p, q)가 필요하다
2. n = p * q
3. ϕ(n) = (p-1) * (q-1)
4. e = e와 ϕ(n)의 서로소
5. d = e*d mod ϕ(n) = 1
6. c = m^e mod n
7. m = c^d mod n

주의 사항

1. 암호화하는 평문은 n의 자릿수보다 작은 자릿수를 가져야한다. a. 평문이 '123456789'이고, n이 '1234'이면 평문을 '123', '456', 789'로 나눠서 암호화해야한다.
2. p와 q는 다음 조건을 만족해야 한다. a. p와 q는 같지 않고 거의 같은 크기의 자릿수야야 한다. b. p-1과 q-1은 커다란 소인수를 각각 가져야 한다. c. p-1과 q-1의 최대 공약수는 작은 수여야 한다

구현하지 않았지만, TMI

1. 실제 RSA에서 사용하는 p와 q는 100자리 정도의 소수로 거의 같은 크기의 자릿수를 가지는 수를 선택한다.

코드

rsa.h

#ifndef _RSA
#define _RSA

typedef struct key
{
    long pkey;  // 초기 2개의 소수 p와 q가 곱해서 나오는 n이 저장될 변수
    long ekey;  // public-key
    long dkey;  // private-key
    int pkey_size;

} Key;

class Rsa
{
public:
    Rsa();
    virtual ~Rsa();

public:
    Key produce_keys();
    long endecrypt(const long msg, const long key, const long pkey);
    int sizeof_int(long data);

private:
    long produce_pkey(const long prime1, const long prime2);
    long produce_ekey(const long orla);
    long produce_dkey(const long ekey, const long orla);
    long produce_prime();
    long produce_orla(const long prime1, const long prime2);
    long produce_gcd(const long a, const long b);
    bool is_prime(const long digit);
};

#endif

main.cpp

#include "rsa.h"
#include <iostream>

using namespace std;

int main(void)
{
    Rsa rsa;
    Key key = rsa.produce_keys();
    cout << "=============================" << endl;
    cout << "=========== R S A ===========" << endl;
    cout << "=============================\n" << endl;

    cout << "=====================================" << endl;
    cout << "암호화 후 얻은 키는 다음과 같습니다."<< endl;
    cout << "n 키 : " << key.pkey << endl;
    cout << "암호화 키 (공개키) : " << key.ekey << endl;
    cout << "암호 해독 키 (개인키) : " << key.dkey << endl;
    cout << "=====================================\n" << endl;
    long msg;
    cout << "암호화할 정보를 입력하십시오 (숫자, 너무 클 수 없음) : ";
    cin >> msg;
    cout << "\n=====================================" << endl;
    long msg_des = rsa.endecrypt(msg, key.ekey, key.pkey);
    cout << "암호화된 정보는 다음과 같습니다 : " << msg_des << endl;
    msg_des = rsa.endecrypt(msg_des, key.dkey, key.pkey);
    cout << "암호 해독된 메시지는 다음과 같습니다 : " << msg_des << endl;
    cout << "=====================================" << endl;
    return 0;
}

rsa.cpp

#include "rsa.h"
#include <cstdlib>
#include <ctime>
#include <string>
#include <bitset>
#include <iostream>

using namespace std;

Rsa::Rsa()
{
}

Rsa::~Rsa()
{
}
/***********************************************************************
암호화 복호화를 동시에 진행하는 메소드
c = m^e mod n
m = c^d mod n
라는 식은 같고 변수만 매개값만 바뀌면 되므로 하나의 메소드에서 처리함
***********************************************************************/
long Rsa::endecrypt(const long msg, const long key, const long pkey)
{
    long msg_des = 1;
    long root = msg;
    long index = key;
    //int n_size = sizeof_int(pkey);
    //int msg_size = sizeof_int(msg);
    //int size = msg_size / n_size;
    //if (msg_size % n_size)
    //  size = size + 1;

    while (index)
    {
        //cout << bitset<32>(index) << endl;
        if (index & 1) {
            msg_des = (msg_des * root) % pkey;
            //cout << "msg_des : " << msg_des << endl;
        }
        index >>= 1;
        //cout << "b root : " << root << endl;
        root = (root * root) % pkey;
        //cout << "a root : " << root << endl;
    }
    return msg_des;
}


/************************************
 p와 q를 생성해서
 n, e, d 키를 생성
 * *********************************/
Key Rsa::produce_keys()
{
    long prime1 = produce_prime();  // p
    long prime2 = produce_prime();  // q
    while (prime2 == prime1)        // p와 q는 n을 만들고 폐기해야 하기 때문에
        prime2 = produce_prime();   // 따로 저장해서 메소드 밖으로 빼지 않음

    Key key;
    long orla = produce_orla(prime1, prime2);   // 오일러 n 생성
    key.pkey = produce_pkey(prime1, prime2);    // n 생성
    key.ekey = produce_ekey(orla);              // e 생성
    key.dkey = produce_dkey(key.ekey, orla);    // d 생성
    return key;
}

/************************************
 N 키 생성
 p * q
 * *********************************/
long Rsa::produce_pkey(const long prime1, const long prime2)
{
    return prime1 * prime2;
}

/************************************
 오일러 n 생성
************************************/
long Rsa::produce_orla(const long prime1, const long prime2)
{
    return (prime1 - 1) * (prime2 - 1);
}

/************************************
 암호화 키 (공개키) e 생성
 * *********************************/
long Rsa::produce_ekey(const long orla)
{
    long ekey;
    while (true)
    {
        ekey = rand() % orla;   // 랜덤 수를 오일러 n으로 나머지 연산
        if (ekey >= 2 && produce_gcd(ekey, orla) == 1)  // e-key와 오일러 n이 서로소인지 판별
            break;
    }
    return ekey;
}

/************************************
 복호화 키 (개인키) d 생성
 * *********************************/
long Rsa::produce_dkey(const long ekey, const long orla)
{
    long dkey = orla / ekey;
    while (true)
    {
        if (((dkey * ekey) % orla) == 1)
            break;
        else 
            ++dkey;
    }
    return dkey;
}

/************************************
 [100, 200] 범위에서 임의의 소수 생성
 * *********************************/
long Rsa::produce_prime()
{
    long prime = 0;
    srand(time(0));
    while (true)
    {
        prime = rand() % 100 + 100;
        if (is_prime(prime))
            break;
    }
    return prime;
}

/************************************
 두 숫자의 최대 공약수 생성        
 * *********************************/
long Rsa::produce_gcd(const long a, const long b)
{
    long dividend = a;
    long divisor = b;
    long residual = dividend % divisor;
    while (residual)
    {
        dividend = divisor;
        divisor = residual;
        residual = dividend % divisor;
    }
    return divisor;
}

/************************************
 소수인지 판단
 * *********************************/
bool Rsa::is_prime(const long digit)
{
    int tmp = 2;
    while (tmp < digit)
        if (!(digit % tmp++))
            break;

    if (tmp == digit)
        return true;
    return false;
}

/************************************
 입력값의 자릿수 판단
 * *********************************/
int Rsa::sizeof_int(long data)
{
    int pos = 1;

    if (data < 0)
        data *= (-1);

    for (int i = 0; ; i++, pos++) {
        if ((data /= 10) <= 0)
            break;
    }

    return pos;
}

결과

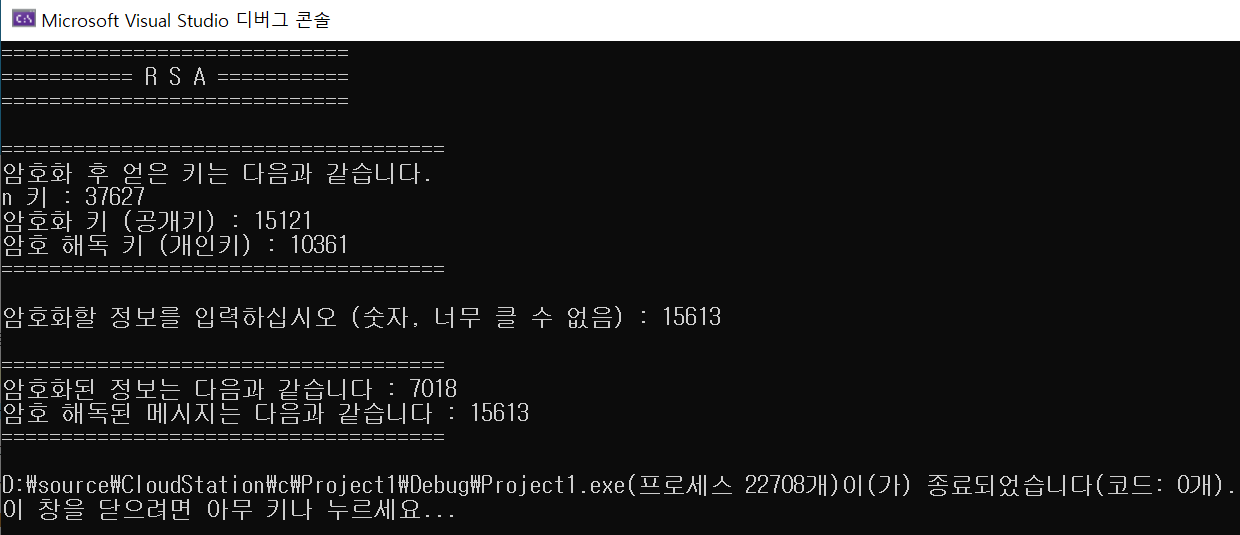
참고문헌

GitHub, "RSA Encryption Decryption", https://github.com/cassvin/Rsa, (2020.06.05.)