[이.취.코] Chap 8. 다이나믹 프로그래밍 - 1로 만들기

1. 1로 만들기

• 난이도
  • 중하
• 풀이 시간
  • 20분
• 시간 제한
  • 1초
• 메모리 제한
  • 128MB

A. 문제

정수 X가 주어진다.
정수 X에 다음 4가지 연산을 사용할 수 있다.

1. X가 5로 나누어떨어지면, 5로 나눈다
2. X가 3로 나누어떨어지면, 3으로 나눈다
3. X가 2로 나누어떨어지면, 2로 나눈다
4. X에서 1을 뺀다

정수 X가 주어졌을 때, 연산 4개를 적절히 사용하여 1을 만든다. 이때 연산을 사용하는 횟수의 최솟값을 구하라.

a. 예를 들면.

정수 26이면, 산을 사용하는 횟수의 최솟값이 3이다.

1. 26 - 1 = 25 (4)
2. 25 / 5 = 5 (1)
3. 5 / 5 = 1 (1)

b. 입력 조건

• 첫째 줄에 정수 X가 주어진다.
  • 1 <= X <= 30,000

c. 출력 조건

• 첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.

d. 테스트 케이스

• 입력 예시

  
  26
  
  

• 출력 예시

  
  3
  
  

B. 내 답안

a. 1차 풀이

x = int(input())  
counts = []  
  
num = [2, 3, 5]  
  
for i in num:  
    count = 0  
    x_2 = x  
    while x_2 > 1:  
        if x_2 >= i:  
            x_2 = (x_2 // i) + (x_2 % i)  
        else:  
            x_2 = x_2 - 1  
    count = count + 1  
    counts.append(count)  
    # print(counts)  
print(min(counts))  
  
# 17분 54초

b. 2차 풀이

x = int(input())
dp = [1e9] * (x+1)
dp[x] = 0

for i in range(x, 0, -1):
    div_5 = 1e9
    div_3 = 1e9
    div_2 = 1e9
    minus_1 = 1e9

    if i % 5 == 0:
        div_5 = dp[i//5]
        # dp[i // 5] = min(dp[i//5], dp[i] + 1)
    if i % 3 == 0:
        div_3 = dp[i//3]
        # dp[i // 3] = min(dp[i//3], dp[i] + 1)
    if i % 2 == 0:
        div_2 = dp[i//2]
        # dp[i // 2] = min(dp[i//2], dp[i] + 1)
    # dp[i-1] = min(dp[i-1], dp[i] + 1)
    minus_1 = dp[i-1]

    dp[i-1] = min(div_5, div_3, div_2, minus_1, dp[i] + 1)

print(dp[1])

c. 회고

풀이

• 신기하게 풀었다.
• DP, 즉 점화식을 사용하지 않고 반복문으로 풀었다.
• 시간복잡도가 크지 않을 것이라 예상해서 반복문을 2개 사용하였다.

반성

• 이 문제를 풀때, DP 파트에 있으니 DP라는 생각은 들었다. 다만 DP를 어떻게 써야하는지 몰랐다.

C. 문제 해설

문제를 풀기 전에 함수가 호출되는 과정을 그림으로 그려보자.

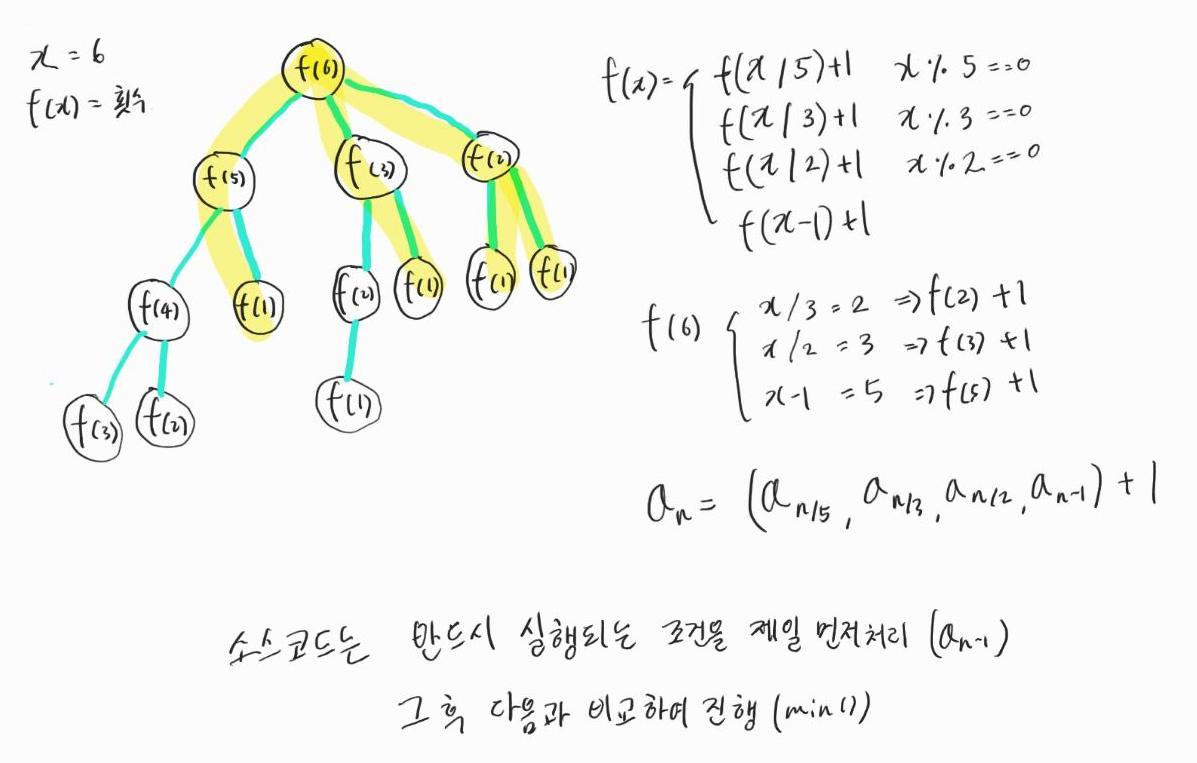
f(2)와 같은 함수들이 동일하게 여러번 호출된다. 이 문제에서 동일한 함수에서 구하는 값들은 동일해야 하므로 다이나믹 프로그래밍을 효과적으로 사용할 수 있다.

점화식으로 표현하면 아래와 같다. 점화식 끝에 1을 더해주는 이유는 함수의 호출 횟수를 구해야 하기 때문이다.

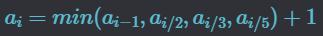
1을 빼는 연산을 제외하고는 해당 수로 나누어떨어질 때에 한해서만 점화식을 적용할 수 있다. 두 수 중 단순히 더 작은 수를 구하고자 할 때는 min() 함수를 이용한다.

a. 책 답안

python-for-coding-test/5.py at master · ndb796/python-for-coding-test (github.com)

참고문헌

나동빈, "이것이 취업을 위한 코딩 테스트다 with 파이썬", 초판, 2쇄, 한빛미디어, 2020년

#코딩테스트 #파이썬 #나동빈 #한빛미디어 #문제 #풀이 #다이나믹프로그래밍 #1로만들기