[이.취.코] Chap 7. 이진 탐색 - 떡볶이 떡 만들기

@mildsalmon·2021-08-23 09:18

1. 떡볶이 떡 만들기

난이도
- 중
풀이 시간
- 40분
시간 제한
- 2초
메모리 제한
- 128MB

A. 문제

떡볶이 떡을 만든다. 떡의 길이가 일정하지 않다. 한 봉지에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰준다.

절단기에 높이(H)를 지정하면 줄지어진 떡을 한 번에 절단한다. 높이가 H보다 긴 떡은 H 위가 잘리고, 낮은 떡은 잘리지 않는다.

손님이 요청한 총 길이가 M이면 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하라.

a. 예를 들면.

높이가 19, 14, 10, 17cm인 떡이 나란히 있다. 절단기 높이를 15cm로 지정하고 자른 뒤 떡의 높이는 15, 14, 19, 15cm가 될 것이고, 잘린 떡의 길이는 4, 0, 0, 2cm이다. 손님은 6cm만큼의 길이를 가져간다.

b. 입력 조건

첫째 줄에 떡의 개수 N과 요청한 떡의 길이 M이 주어진다
- 1 <= N <= 1,000,000
- 1 <= M <= 2,000,000,000
둘째 줄에는 떡의 개별 높이가 주어진다.
- 떡 높이의 총합은 항상 M 이상이므로, 손님은 필요한 양만큼 떡을 사갈 수 있다
- 높이는 10억보다 작거나 같은 양의 정수 또는 0이다.

c. 출력 조건

적어도 M만큼의 떡을 집에 가져가기 위해 절단기에 설정할 수 있는 높이의 최댓값을 출력하라.

d. 테스트 케이스

입력 예시
```
4 6
19 15 10 17
```
출력 예시
```
15
```

B. 내 답안


n, m = list(map(int, input().split()))  
array = list(map(int, input().split()))  
  
array.sort(reverse=True)  
  
m2 = 0  
  
while(m > m2):  
    max_value = max(array)  
    for i in range(len(array)):  
        if array[i] == max_value:  
            array[i] = array[i] - 1  
    m2 = m2 + 1  
    # print("array : ", array)  
    # print("m2 : ", m2)  
result = max(array)  
  
print(result)

a. 회고

풀이

떡의 개수 N은 최대 100만개, 요청한 떡의 길이 M은 최대 20억개. 따라서 떡의 개수의 시간 복잡도는 O(nlogn), O(n), O(logn)여야 1초 안에 동작한다. 요청한 떡의 길이의 시간 복잡도는 O(logn)이 되어야 시간 제한 안에 동작한다.

다만, 이 문제를 이진 탐색으로 푸는 방법이 생각나지 않았다. 그래서 단순하게 풀었는데, 내가 푼 방식의 시간 복잡도는 O(4m) 이다. 내 방식은 m에 의해 결정되므로 O(logm)이어야 시간 제한 안에 풀 수 있지만, 그러지 못했다.

반성

떡의 길이에 이진 탐색을 적용할 수 있다고 생각하지 못했다.

이진 탐색을 제대로 구현하는 부분도 아직 많이 부족하다고 느낀다.

C. 문제 해설

이진 탐색 문제이자, 파라메트릭 서치(Parametric Search) 유형의 문제이다. 파라메트릭 서치는 최적화 문제를 결정 문제로 바꾸어 해결하는 기법이다. 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제에 주로 파라메트릭 서치를 사용한다.

최적화 문제라면 이진 탐색으로 결정 문제를 해결하면서 범위를 좁혀갈 수 있다. 코딩테스트나 프로그래밍 대회에서는 보통 파라메트릭 서치 유형은 이진 탐색을 이용하여 해결한다.

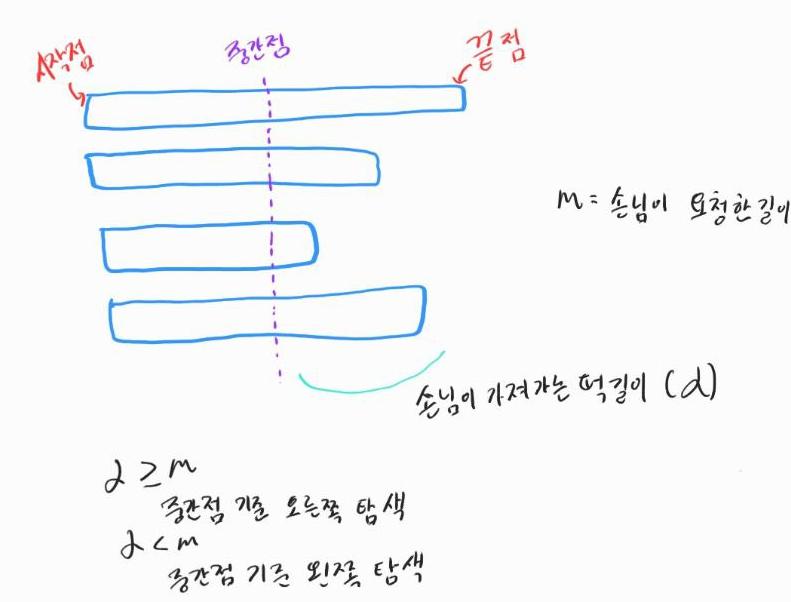
이 문제의 풀이 아이디어는 적절한 높이를 찾을 때까지 절단기의 높이 H를 반복해서 조정하는 것이다. 현재 이 높이를 자르면 조건을 만족할 수 있는가? 를 확인한 뒤에 조건의 만족 여부에 따라서 탐색 범위를 좁혀서 해결할 수 있다. 범위를 좁힐 때는 이진 탐색의 원리를 이용하여 절반씩 탐색 범위를 좁혀 나간다.

절단기의 높이는 1부터 10억까지의 정수 중 하나인데, 이처럼 큰 수를 보면 당연하다는듯이 가장 먼저 이진 탐색을 떠올려야 한다.

높이 H를 이진 탐색으로 찾는다면, 대략 31번 만에 경우의 수를 모두 고려할 수 있다. 떡의 개수 N은 최대 100만 개이므로 이진 탐색으로 절단기의 높이 H를 바꾸면서, 바꿀 때마다 모든 떡을 체크하는 경우 대략 최대 3,000만 번 정도의 연산으로 문제를 풀 수 있다.

문제의 시간 제한은 2초이므로 3,000만 번 정도의 연산이 필요하다면 시간 초과를 받지 않을 수 있다.