Chap 18. 그래프이론 - Q44. 행성 터널

@mildsalmon·2021-12-02 15:13

1. 행성 터널

난이도
- 중
풀이 시간
- 40분
시간 제한
- 1초
메모리 제한
- 128MB
출처
- 2887번: 행성 터널 (acmicpc.net)

A. 📜 문제

위 백준 사이트에 접속하여 문제를 확인해주세요.

B. 💡 내 답안

a. 😅 1차 시도 (실패 - 메모리 오류)


def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)

    if a > b:
        parent[a] = b
    else:
        parent[b] = a

n = int(input())

planets = []
tunnels = []
parent = [i for i in range(n)]
total_cost = 0

for i in range(n):
    x_a, y_a, z_a = list(map(int, input().split()))

    if i >= 1:
        for j in range(len(planets)):
            x_b, y_b, z_b = planets[j]

            cost = min(abs(x_a - x_b), abs(y_a - y_b), abs(z_a - z_b))
            tunnels.append((cost, i, j))

    planets.append((x_a, y_a, z_a))

tunnels.sort()

for tunnel in tunnels:
    cost, a, b = tunnel

    if find_parent(parent, a) != find_parent(parent, b):
        union_parent(parent, a, b)
        total_cost += cost

print(total_cost)

b. 😊 2차 시도 (성공)


def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)

    if a > b:
        parent[a] = b
    else:
        parent[b] = a

n = int(input())

planets_x = []
planets_y = []
planets_z = []
tunnels = []
parent = [i for i in range(n)]
total_cost = 0

for i in range(n):
    x, y, z = list(map(int, input().split()))

    planets_x.append((x, i))
    planets_y.append((y, i))
    planets_z.append((z, i))

planets_x.sort()
planets_y.sort()
planets_z.sort()

for i in range(n-1):
    tunnels.append((planets_x[i+1][0] - planets_x[i][0], planets_x[i][1], planets_x[i+1][1]))
    tunnels.append((planets_y[i+1][0] - planets_y[i][0], planets_y[i][1], planets_y[i+1][1]))
    tunnels.append((planets_z[i+1][0] - planets_z[i][0], planets_z[i][1], planets_z[i+1][1]))

tunnels.sort()

for tunnel in tunnels:
    cost, a, b = tunnel

    if find_parent(parent, a) != find_parent(parent, b):
        union_parent(parent, a, b)
        total_cost += cost

print(total_cost)

c. 🙄 회고

내 풀이

쉽게 생각했다.
- 새로운 행성이 들어오면, 이전에 들어온 행성들과의 거리를 구한 다음, 그 중 최솟값을 저장하는 방식으로 1차 시도를 했었다.

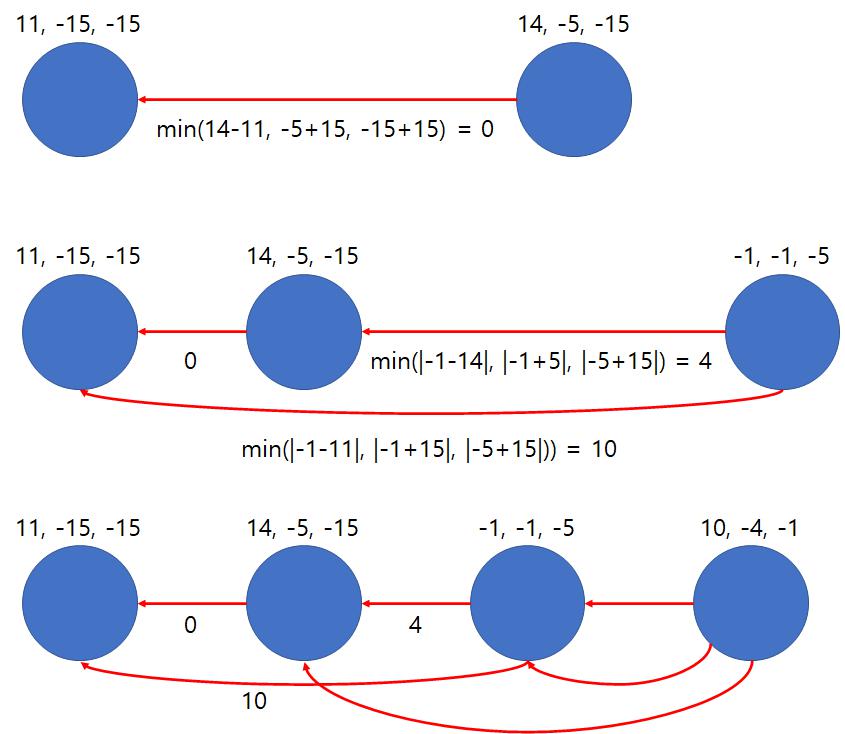
그러면, 위와 같은 방식으로 계산되는데, 이 경우 간선의 개수가 (n(n+1)/2)개 나온다.
- 그러나, 문제에서 제시된 행성의 최대 개수가 100,000개이므로, 메모리 초과, 시간 초과가 발생한다.

반성

단순히 알고리즘만 떠올리고 제약조건을 확인하지 못했다.

결론

제약조건들도 고려를 해보자.

C. 🧐 문제 해설

이해한 내용을 바탕으로 작성했습니다.

x, y, z 좌표가 아래와 같이 주어진다고 생각해보자.

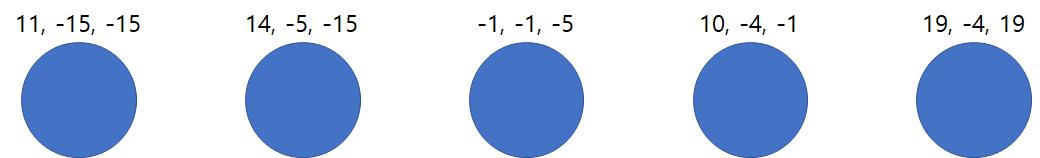
위의 회고에서 x, y, z를 한꺼번에 계산하는 방식을 시도했다가 실패했으니, 이번에는 각 좌표에서 x, y, z를 따로 분리해서 생각해보자.

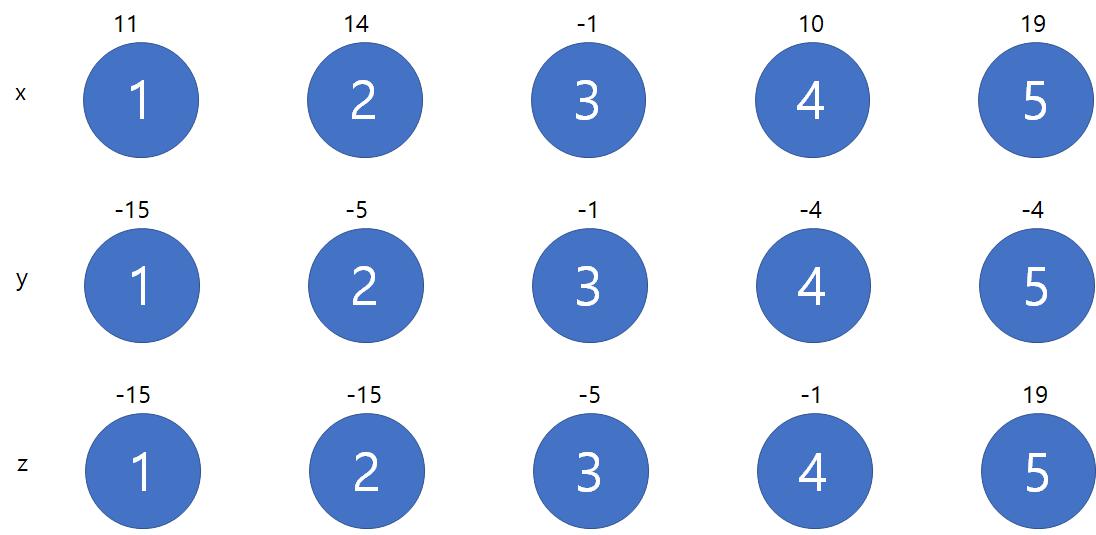
분리된 x좌표를 정렬하면 아래와 같다.

이때, 각 좌표는 선형적으로 존재하므로, i+1 - i가 각 좌표 사이의 최소거리가 된다.

이렇게 (n-1)번의 연산만으로 각 좌표 사이의 최소 거리를 구할 수 있다. 이제 나머지 y, z를 이런 방식으로 구하면, 3*(n-1)이 된다.

이제 회고에서 푼 방식의 코드와 문제 해설에서 설명하는 코드를 비교하면서 시간복잡도를 계산해보자.

1) 회고에서 푼 방식


for i in range(n):  
    x_a, y_a, z_a = list(map(int, input().split()))  
  
    if i >= 1:  
        for j in range(len(planets)):  
            x_b, y_b, z_b = planets[j]  
  
            cost = min(abs(x_a - x_b), abs(y_a - y_b), abs(z_a - z_b))  
            tunnels.append((cost, i, j))  
  
    planets.append((x_a, y_a, z_a))

시간복잡도가 O($n^2$)이다.

2) 문제 해설에서 설명한 방식


for i in range(n):
    x, y, z = list(map(int, input().split()))

    planets_x.append((x, i))
    planets_y.append((y, i))
    planets_z.append((z, i))

planets_x.sort()
planets_y.sort()
planets_z.sort()

for i in range(n-1):
    tunnels.append((planets_x[i+1][0] - planets_x[i][0], planets_x[i][1], planets_x[i+1][1]))
    tunnels.append((planets_y[i+1][0] - planets_y[i][0], planets_y[i][1], planets_y[i+1][1]))
    tunnels.append((planets_z[i+1][0] - planets_z[i][0], planets_z[i][1], planets_z[i+1][1]))