1. 화성 탐사
- 난이도
- 중
- 풀이 시간
- 40분
- 시간 제한
- 1초
- 메모리 제한
- 128MB
- 기출
- ACM-ICPC
A. 📜 문제
당신은 화성 탐사 기계를 개발하는 프로그래머다. 그런데 화성은 에너지 공급원을 찾기가 힘들다. 그래서 에너지를 효율적으로 사용하고자 화성 탐사 기계가 출발 지점에서 목표 지점까지 이동할 때 항상 최적의 경로를 찾도록 개발해야 한다.
화성 탐사 기계가 존재하는 공간은 N x N 크기의 2차원 공간이며, 각각의 칸을 지나기 위한 비용(에너지 소모량)이 존재한다. 가장 왼쪽 위 칸인 [0][0] 위치에서 가장 오른쪽 아래 칸인 [N - 1][N - 1] 위치로 이동하는 최소 비용을 출력하는 프로그램을 작성하라. 화성 탐사 기계는 특정한 위치에서 상하좌우 인접한 곳으로 1칸씩 이동할 수 있다.
a. 입력 조건
- 첫째 줄에 테스트 케이스의 수 T(1 <= T <= 10)가 주어진다.
- 매 테스트 케이스의 첫째 줄에는 탐사 공간의 크기를 의미하는 정수 N이 주어진다.
- 2 <= N <= 125
- 이어서 N개의 줄에 걸쳐 각 칸의 비용이 주어지며 공백으로 구분한다.
- 0 <= 각 칸의 비용 <= 9
c. 출력 조건
- 각 테스트 케이스마다 [0][0]의 위치에서 [N - 1][N - 1]의 위치로 이동하는 최소 비용을 한 줄에 하나씩 출력한다.
d. 테스트 케이스
입력 예시
3 3 5 5 4 3 9 1 3 2 7 5 3 7 2 0 1 2 8 0 9 1 1 2 1 8 1 9 8 9 2 0 3 6 5 1 5 7 9 0 5 1 1 5 3 4 1 2 1 6 5 3 0 7 6 1 6 8 5 1 1 7 8 3 2 3 9 4 0 7 6 4 1 5 8 3 2 4 8 3 7 4 8 4 8 3 4출력 예시
20 19 36
B. 💡 내 답안
a. 😅 1차 시도 (실패)
"""
Date : 2021.11.25
Update : 2021.11.25
Source : Q39_화성탐사.py
Purpose :
Author : 김학진 (mildsalmon)Email : mildsalmon@gamil.com
"""
from collections import deque
def dfs(i, j):
ds = ((0, 1), (0, -1), (1, 0), (-1, 0))
for d in ds:
dx = i + d[0]
dy = j + d[1]
if 0 <= dx < n and 0 <= dy < n:
temp_graph[dx][dy] = min(temp_graph[dx][dy], temp_graph[i][j] + graph[dx][dy])
dfs(dx, dy)
for t in range(int(input())):
# 탐사 공간
n = int(input())
graph = []
for i in range(n):
temp = list(map(int, input().split()))
graph.append(temp)
temp_graph = [[1e9] * n for _ in range(n)]
for i in range(n):
for j in range(n):
dfs(i, j)
q = deque()
q.append((0, 0))
while q:
x, y = q.popleft()
for d in ds:
dx = x + d[0]
dy = y + d[1]
if 0 <= dx < n and 0 <= dy < n:
if temp_graph[dx][dy] == 1e9:
q.append((dx, dy))
temp_graph[dx][dy] = min(temp_graph[dx][dy], temp_graph[x][y] + graph[dx][dy])
print(*temp_graph, sep='\n')
print(temp_graph[n-1][n-1])
# for k in range(n):
# for i in range(n):
# for j in range(n):
# graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
#
# print(graph[n-1][n-1])
b. 😊 2차 풀이 (성공)
import heapq
for t in range(int(input())):
# 탐사 공간
n = int(input())
# 탐사 공간에 대한 비용
graph = []
for i in range(n):
graph.append(list(map(int, input().split())))
# 다익스트라를 위한 q
q = []
heapq.heappush(q, (graph[0][0], 0, 0))
# 상하좌우 탐색을 위한 ds
ds = ((0, 1), (0, -1), (1, 0), (-1, 0))
distance = [[1e9] * n for _ in range(n)]
distance[0][0] = graph[0][0]
while q:
dist, x, y = heapq.heappop(q)
if distance[x][y] < dist:
continue
for d in ds:
dx = x + d[0]
dy = y + d[1]
if 0 <= dx and dx < n and 0 <= dy and dy < n:
cost = dist + graph[dx][dy]
if cost < distance[dx][dy]:
distance[dx][dy] = cost
heapq.heappush(q, (cost, dx, dy))
print(distance[n-1][n-1])
b. 🙄 회고
내 풀이
- 처음에는 플로이드로 접근했다가, 접근 방식이 잘못된 것을 느꼈다.
- 그래서 dfs, bfs를 사용해봤는데, 연산값이 [0][0]부터 진행되어 온 최솟값인지 파악하기가 어려웠다.
결론
- 인접 행렬로 생각하지말고, 그냥 행렬의 모든 칸을 노드라고 생각하고 다익스트라로 풀었어야했다..
C. 🧐 문제 해설
이해한 내용을 바탕으로 작성했습니다.
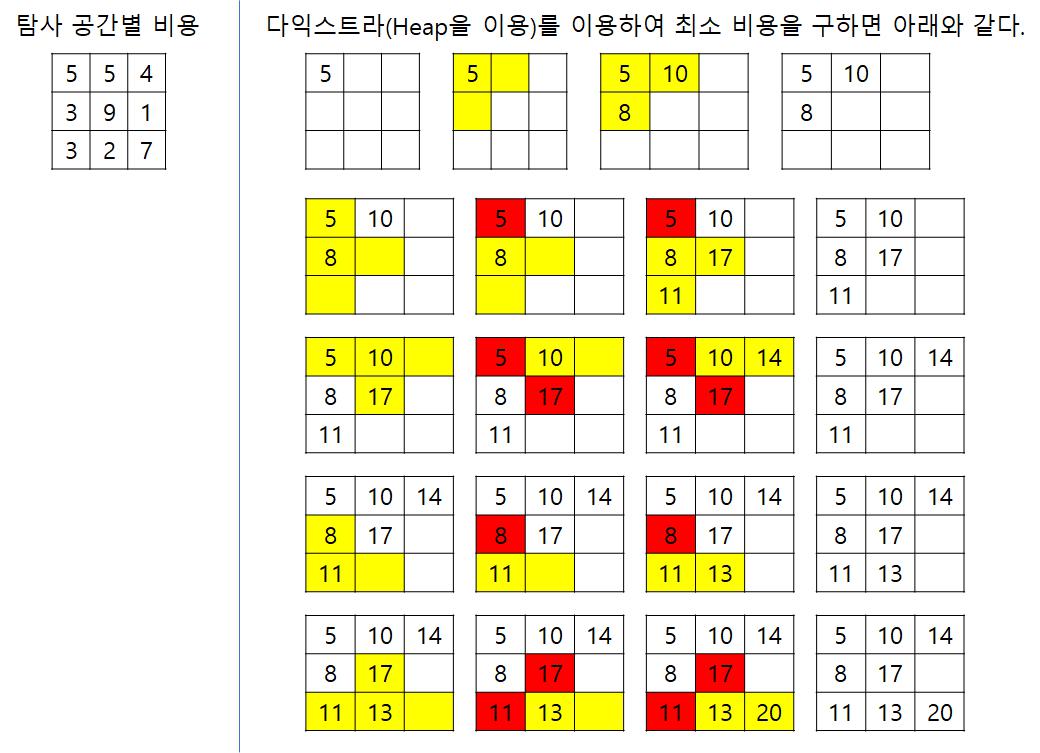
a. 책 답안
python-for-coding-test/3.py at master · ndb796/python-for-coding-test (github.com)
참고문헌
[1] 나동빈, "이것이 취업을 위한 코딩 테스트다 with 파이썬", 초판, 2쇄, 한빛미디어, 2020년