1. 정수 삼각형
- 난이도
- 중하
- 풀이 시간
- 30분
- 시간 제한
- 2초
- 메모리 제한
- 128 MB
- 출처
A. 📜 문제
- 중하
- 30분
- 2초
- 128 MB
위 백준 사이트에 접속하여 문제를 확인해주세요.
B. 💡 내 답안
a. 😊 1차 시도 (성공)
n = int(input())
array = [[] for i in range(n)]
for i in range(n):
temp = list(map(int, input().split()))
array[i] = temp
dp = [i[:] for i in array]
dp[0] = array[0]
for i in range(1, n):
for j in range(len(array[i])):
if len(dp[i-1])-1 < j:
dp[i][j] = dp[i-1][j-1] + array[i][j]
elif j-1 < 0:
dp[i][j] = dp[i-1][j] + array[i][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + array[i][j]
print(max(dp[-1]))
b. 🙄 회고
내 풀이
- 31번 문제처럼 DP를 사용하였다.
반성
- 이 글을 쓰면서 코드를 다시 보는데, 해석하기 난해하다. 그리고 좀 잘못푼 것 같다.
- if-elif-else로 구성하면, 윗층에 값을 한 개밖에 비교를 못할텐데 뭔가 이상하게 코드를 짯다.
C. 🧐 문제 해설
이해한 내용을 바탕으로 작성했습니다.
n = int(input())
array = [[] for i in range(n)]
for i in range(n):
temp = list(map(int, input().split()))
array[i] = temp
dp = [i[:] for i in array]
dp[0] = array[0]
for i in range(1, n):
for j in range(len(array[i])):
if len(dp[i-1])-1 < j:
dp[i][j] = dp[i-1][j-1] + array[i][j]
elif j-1 < 0:
dp[i][j] = dp[i-1][j] + array[i][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + array[i][j]
print(max(dp[-1]))
b. 🙄 회고
내 풀이
- 31번 문제처럼 DP를 사용하였다.
반성
- 이 글을 쓰면서 코드를 다시 보는데, 해석하기 난해하다. 그리고 좀 잘못푼 것 같다.
- if-elif-else로 구성하면, 윗층에 값을 한 개밖에 비교를 못할텐데 뭔가 이상하게 코드를 짯다.
C. 🧐 문제 해설
이해한 내용을 바탕으로 작성했습니다.
내 풀이
반성
- if-elif-else로 구성하면, 윗층에 값을 한 개밖에 비교를 못할텐데 뭔가 이상하게 코드를 짯다.
이해한 내용을 바탕으로 작성했습니다.
문제를 풀면 아래처럼 풀리게 된다.
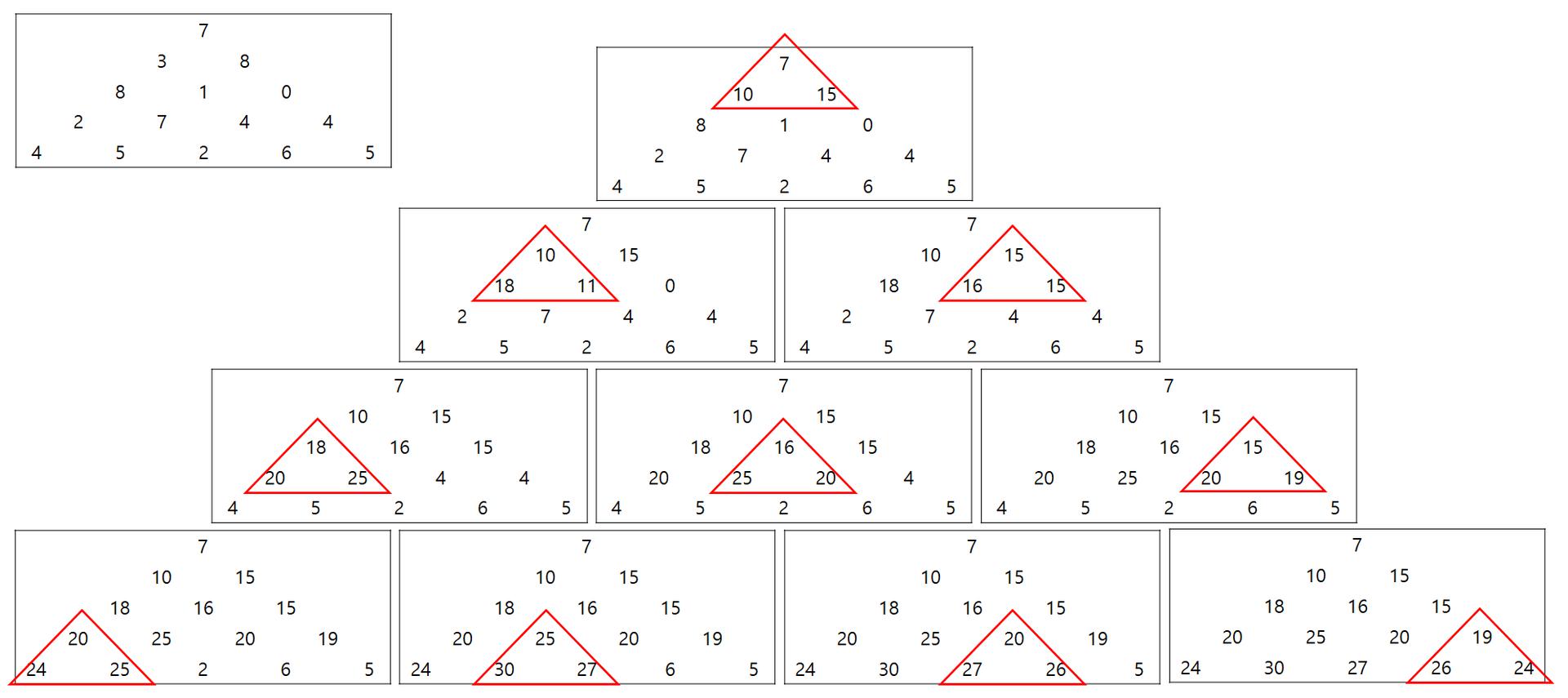
다만, 저런식으로 입력 리스트를 피라미드 형태로 구성하면서 풀기보다, 리스트에 어떤 모양으로 들어갈지 생각해서 푸는게 더 편하다.
2차원 리스트를 생각하면 이렇게 값이 들어간다.
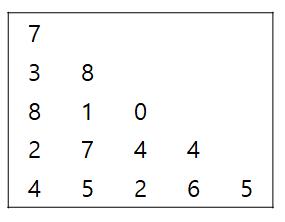
그럼 값은 아래처럼 계산할 수 있다.
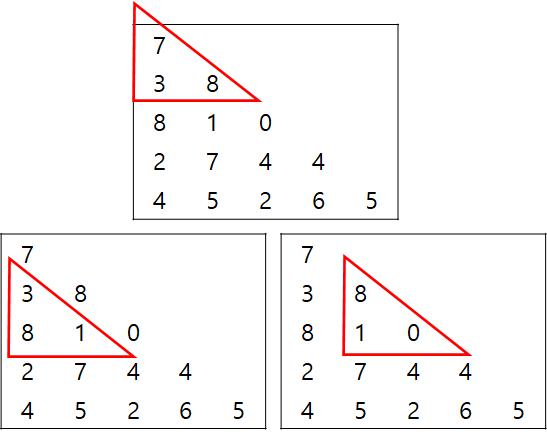
그런데, 31번에서 푼 방식처럼, 아랫층 값을 구성할 수 있는 윗층 값들을 비교한 후 더 큰 값과 아랫층 값을 더해서 최상의 결과를 구하는 것이 연산 횟수도 적고, 빠르지 않을까?
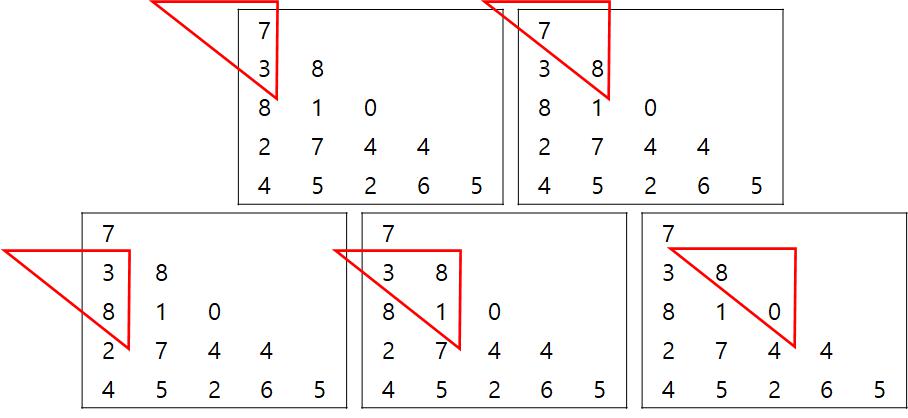
그럼 $dp_{(n, m)} = max(dp_{(n-1, m-1)}, dp_{(n-1, m)}) + array_{(n, m)}$ 이런 공식이 나온다.
a. 책 답안
python-for-coding-test/2.py at master · ndb796/python-for-coding-test (github.com)
참고문헌
나동빈, "이것이 취업을 위한 코딩 테스트다 with 파이썬", 초판, 2쇄, 한빛미디어, 2020년
1932번: 정수 삼각형 (acmicpc.net). Baekjoon. (accessed Oct 24, 2021)
Ghost