1. 결혼식
- 난이도
- 실버 2
- 시간 제한
- 1초
- 메모리 제한
- 128 MB
- 출처
A. 📜 문제
위 백준 사이트에 접속하여 문제를 확인해주세요.
B. 💡 내 답안
a. 😅 1차 시도 (실패 - 단방향만 고려함)
# 다익스트라
# 최단거리
# 최단 거리가 2 이하인 경우만 구함 (친구, 친구의 친구)
import heapq
n = int(input())
m = int(input())
graph = [[] for i in range(n+1)]
for i in range(m):
a, b = list(map(int, input().split()))
graph[a].append(b)
graph[b].append(a)
distance = [1e9] * (n+1)
distance[1] = 0
q = []
heapq.heappush(q, (1, 0))
while q:
node, cost = heapq.heappop(q)
if distance[node] < cost:
continue
for next_node in graph[node]:
next_cost = cost + 1
if next_cost < distance[next_node]:
distance[next_node] = next_cost
heapq.heappush(q, (next_node, next_cost))
count = 0
for i in range(2, len(distance)):
if distance[i] <= 2:
count += 1
print(count)
반례
10 10 4 10 7 10 3 7 6 8 1 7 1 6 1 5 1 9 2 4 3 8
b. 😊 2차 시도 (성공)
# 다익스트라
# 최단거리
# 최단 거리가 2 이하인 경우만 구함 (친구, 친구의 친구)
import heapq
n = int(input())
m = int(input())
graph = [[] for i in range(n+1)]
for i in range(m):
a, b = list(map(int, input().split()))
# 주어진 친구를 graph로 입력받는다.
graph[a].append(b)
# 이 부분에서 A-B가 친구이면 B-A도 친구인 것을 인지했어야 한다.
graph[b].append(a)
# 친구들의 최단 거리를 저장하는 dp
distance = [1e9] * (n+1)
# 상근이(나)의 최단 거리 초기화
distance[1] = 0
# 다익스트라 알고리즘에서는 보통 heap을 사용한다.
# 우선순위가 높은 것부터 삭제해야지 불필요한 연산이 진행되지 않기 때문이다.
# 하지만, graph 값으로 가지고 있는 것은 나와 친구인 node 번호만 가지고 있기 때문에 우선순위를 매길 것이 없다.
# 따라서, 단순 list로 구현해도 충분했을 것 같다.
q = []
heapq.heappush(q, (1, 0))
while q:
# 우선순위가 가장 높은 node pop
node, cost = heapq.heappop(q)
# 저장된 현재 node의 최단 거리가 pop한 cost(최단거리)보다 작다면 continue
if distance[node] < cost:
continue
# graph의 현재 node와 연결된 다른 node들을 탐색
for next_node in graph[node]:
# 최단 거리는 현재 node의 최단 거리 + 1로 증가한다.
next_cost = cost + 1
# 저장된 다음 node의 최단 거리가 next_cost보다 크다면 최단거리 갱신 및 heap에 추가
if next_cost < distance[next_node]:
distance[next_node] = next_cost
heapq.heappush(q, (next_node, next_cost))
count = 0
# 최단 거리가 2 이하인 경우만 구함.
# 친구 = 1, 친구의 친구 = 2
for i in range(2, len(distance)):
if distance[i] <= 2:
count += 1
print(count)
a. 🙄 회고
내 풀이
- 뭔가 다른 방법이 있어보였는데, 다익스트라가 보여서 다익스트라로 풀었다.
반성
- 양방향을 생각하지 못했다.
- 단방향만 고려하여 풀었을 때의 반례는 아래 해설에서 설명한다.
C. 🧐 문제 해설
이해한 내용을 바탕으로 작성했습니다.
10
10
4 10
7 10
3 7
6 8
1 7
1 6
1 5
1 9
2 4
3 8
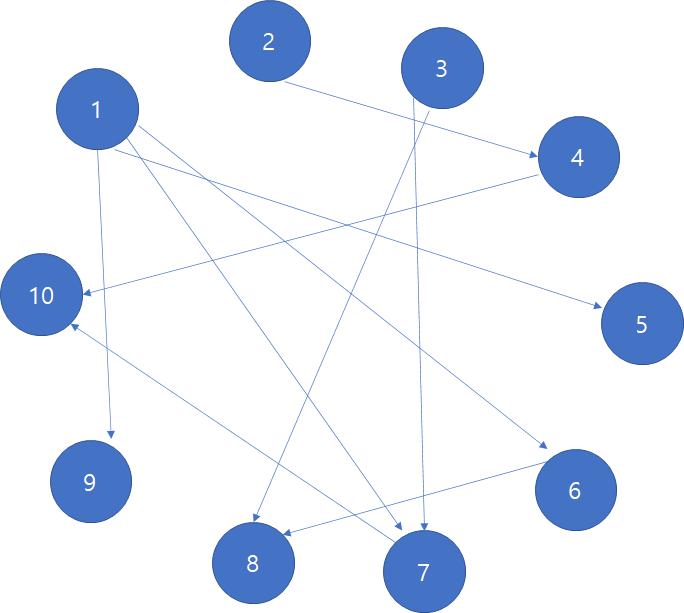
단방향으로만 생각하면 이런식으로 그림이 그려진다.
이 경우 친구(빨간색)와 친구의 친구(초록색)를 표현하면 아래와 같다.
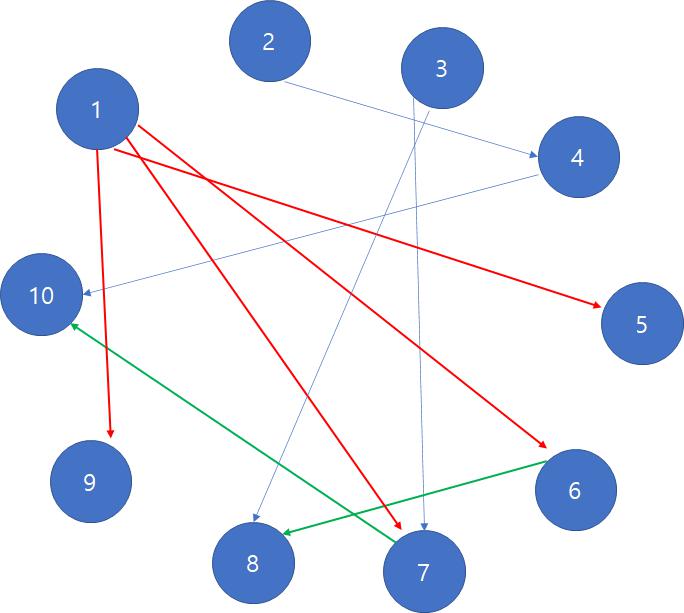
따라서 친구와 친구의 친구는 총 6명이다.
그런데 뭔가 이상하다.
3-7은 친구의 친구가 아닌 것일까?
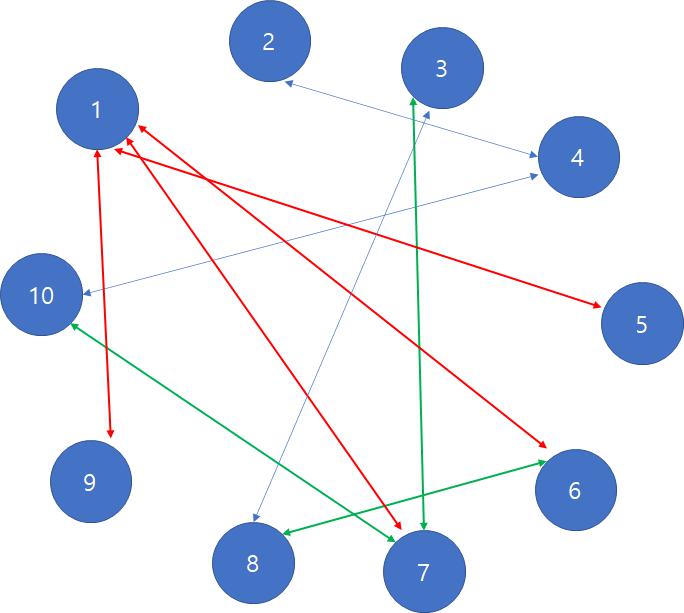
이처럼 단방향만 고려한다면 3 -> 7은 친구의 친구로 고려되지 않는다.
따라서 7의 친구는 10만 존재하게 된다.
하지만 친구는 양방향으로 성립되기 때문에 7의 친구는 10과 3이 존재해야 한다.
그래서 2차 시도 코드처럼 수정하면 문제가 해결된다.
참고문헌
[1] baekjoon. 1065번: 한수 (acmicpc.net). Baekjoon. (accessed Dec 22, 2021)
[2] 문제 3. JOI 2009-2010 자격 질문 및 데이터 (ioi-jp.org). JOI. (accessed Dec 22, 2021)