Summer/Winter Coding(2019) - 멀쩡한 사각형

1. 멀쩡한 사각형

• 난이도
  • Level 2
• 출처
  • 코딩테스트 연습 - 멀쩡한 사각형 | 프로그래머스 (programmers.co.kr)

A. 📜 문제

위 프로그래머스 사이트에 접속하여 문제를 확인해주세요.

B. 💡 내 답안

a. 😅 1차 시도 (실패)

def solution(w,h):
    total_count = w * h
    
    if w == 1 or h == 1:
        return 0
    
    if w % h == 0:
        return total_count - h * (w // h)
    
    if h % w == 0:
        return total_count - w * (h // w)

채점 결과

정확성: 50.0

합계: 50.0 / 100.0

b. 😊 2차 시도 (성공)

import math


def solution(w, h):
    gcd = math.gcd(w, h)
    
    if gcd == 1:
        answer = w + h - 1
    elif gcd > 1:
        answer = gcd * ((w // gcd) + (h // gcd) - 1)
    
    return w * h - answer

c. 🙄 회고

내 풀이

• 내 손으로 그리는 그림은 완전한 정사각형이 아니라서 ppt를 통해 그려보면서 풀었다.
• w와 h를 1부터 늘려가는 방법으로 풀었다.
  • w 혹은 h가 1이면 모든 칸이 대각선 방향으로 잘려서 사용할 수 있는 사각형이 없다.
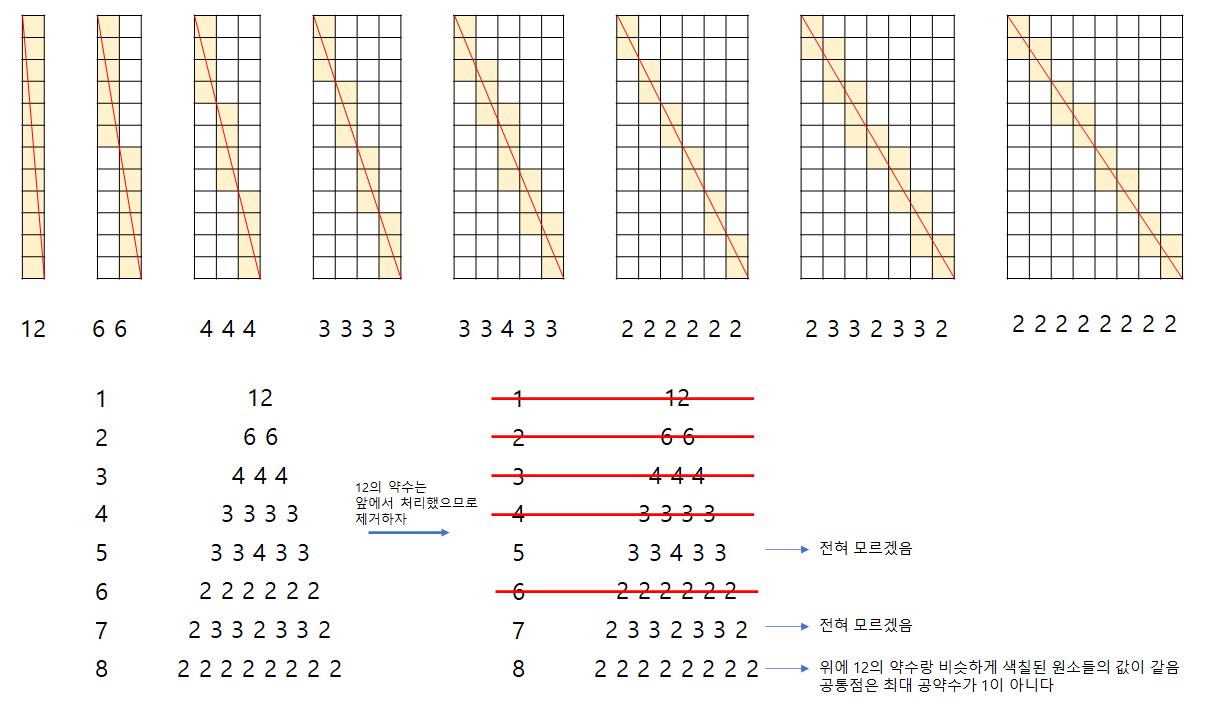
  • h를 2에 고정하고 w만 늘려보자.
    • w가 h(2)의 배수가 되는 경우에만 사각형이 딱 나눠 떨어진다.
    • 색칠된 칸 중 겹치는 칸이 없으므로 한 행에 색칠되는 칸을 구하고 행을 곱하면 값이 나온다.
    • 이것을 공식으로 풀어보면, (w // h * h) 이다.
  • w가 h의 배수가 되지 않는 경우에는 값의 패턴을 발견하기 힘들었다.

반성

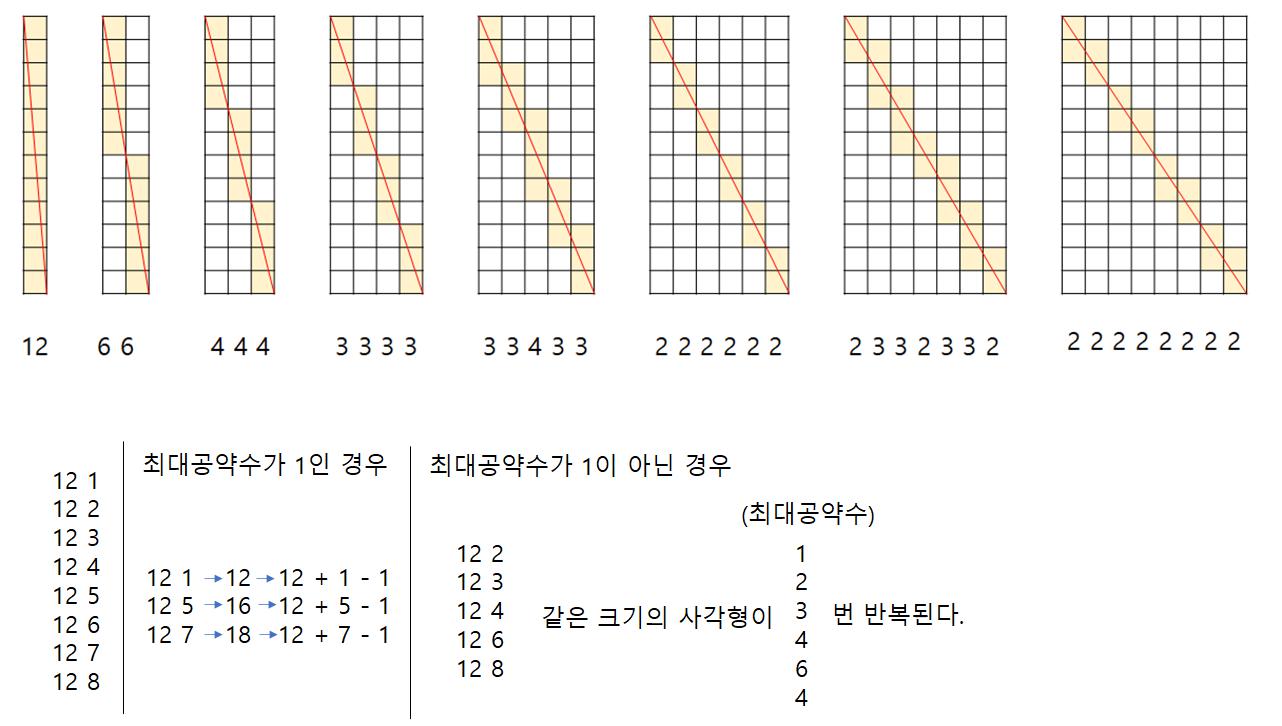
• 애초에 배수로 접근하면 풀리지 않는 문제였다.
• 문제를 보고 수학이라는 느낌은 왔지만, 한번에 최대공약수가 떠오르지는 않았다.

결론

• 뭐... 많이 풀어봐야겠다. 다른 방법이 없다.

C. 🧐 문제 해설

이해한 내용을 바탕으로 작성했습니다.

참고문헌

Summer/Winter Coding(2019). 코딩테스트 연습 - 멀쩡한 사각형 | 프로그래머스 (programmers.co.kr). Programmers. (accessed Oct 12, 2021)