넘파이
- 넘파이 : 행렬이나 다차원 배열을 쉽게 처리하거나 수치 계산을 위한 라이브러리로, 다차원 리스트나 크기가 큰 데이터 처리에 유리함
import numpy as np # numpy 모듈 호출
넘파이의 특징
- 속도가 빠르고 메모리 사용이 효율적 : 데이터를 메모리에 할당하는 방식이 기존과 다름
- 반복문을 사용하지 않음 : 연산할 때 병렬로 처리하며, 함수를 한 번에 많은 요소에 적용
- 다양한 선형대수 관련 함수 제공
- C, C++, 포트란 등 다른 언어와 통합 사용 가능
넘파이 함수
넘파이 배열 객체
넘파이 배열(ndarray) : 넘파이에서 텐서 데이터를 다루는 객체
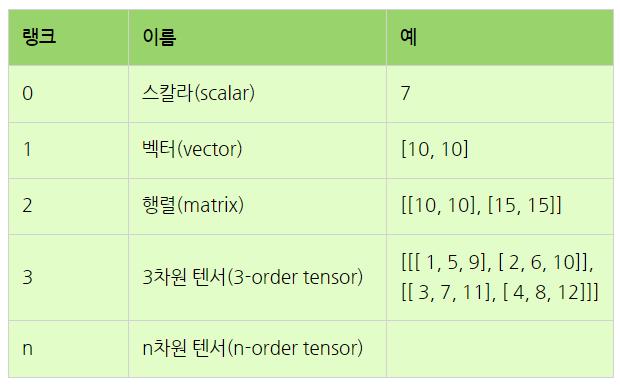
텐서(tensor) : 선형대수의 데이터 배열로 랭크에 따라 이름이 다름

np. array : 넘파이 배열 생성
import numpy as np
test_array = np.array([넘파이 배열 정보], dtype=저장하는 데이터 타입)
파이썬 리스트와 넘파이 배열의 차이점
- 텐서 구조에 따라 배열 생성 : 배열의 모든 구성 요소에 값이 존재
- 파이썬에서는 동적 타이핑을 지원하나, 넘파이에서는 동적 타이핑을 지원하지 않음
- 하나의 데이터 타입만 사용
- 하나의 형태로 자동 형 변환
- 데이터를 메모리에 연속적으로 나열
- 각 값의 메모리 크기가 동일
- 검색이나 연산 속도가 리스트에 비해 빠름
- 데이터 배열을 생성할 때 원하는 데이터 타입을 넣거나 우선 순위(int < float < complex < str)에 의해 자동 형 변환이 이루어짐
test = np.array([1, 2, 4, "7"], float)
print(test) # [1., 2., 4., 7.]
- type : 데이터 타입을 확인할 수 있음
print(type(test)) # <class 'numpy.ndarray'>
print(type(test[3])) # <class 'numpy.float64'>
- dtype : 넘파이 배열 매개변수나 데이터 타입 반환
print(test.dtype) # float64
test = np.array([1, 2, 4, "7"], dtype=float) # 데이터 타입을 지정해주는 매개변수로도 사용
print(test) # [1., 2., 4., 7.]
- shape : 넘파이 배열 차원 구조를 튜플로 반환
print(test.shape) # (4, )
test = np.array([[1, 4, 5, 2, "1"],
[2, 1, 4, 9, 5]], float)
print(test.shape) # (2, 5) (행, 열)
test = [
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]]
]
np.array(test, int).shape # (4, 3, 4) (면, 행, 열)
- ndim : 넘파이 배열의 차원 개수를 반환
test = [
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]]
]
np.array(test, int).ndim # 3
- size : 넘파이 배열의 원소의 개수를 반환
test = [
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]]
]
np.array(test, int).size # 48
- itemsize : 넘파이 배열에서 각 요소가 차지하는 바이트 확인
np.array( [[1, 4, 5, 2, 1],
[2, 1, 4, 9, 5]], dtype=np.float64).itemsize # 8
np.array( [[1, 4, 5, 2, 1],
[2, 1, 4, 9, 5]], dtype=np.float32).itemsize # 4
- reshape : 배열의 구조와 차원 변경하며, 배열의 형태와 전체 요소 개수가 맞아야
test = np.array( [[1, 4, 5, 2],
[2, 1, 4, 9]])
test.shape # (2, 4)
# -1을 사용하면 나머지 지정된 차원과 전체 요소 개수를 고려해 차원이 자동 지정
test.reshape(-1, ) # array([1, 4, 5, 2, 2, 1, 4, 9])
test.reshape(2, -1) # array([[1, 4, 5, 2], [2, 1, 4, 9]])
test.reshape(2, 2, -1) # array([[[1, 4], [5, 2]], [[2, 1], [4, 9]]])
test = np.array([1, 4, 5, 2, 1, 2, 1, 4, 9, 5])
test.shape # (10,)
test.reshape(5,2) # array([[1, 4], [5, 2], [1, 2], [1, 4], [9, 5]])
- flatten : 데이터 순서대로 1차원으로 변경
test = np.array([[[1, 4],
[5, 2]],
[[2, 1],
[4, 9]]])
test.flatten() # array([1, 4, 5, 2, 2, 1, 4, 9])
- 인덱싱(indexing) : 기준으로부터 떨어진 값에 접근, [행][열] 또는 [행, 열] 형태로 지원
test = np.array([[[1, 4],
[5, 2]],
[[2, 1],
[4, 9]]])
test[0] # array([[1, 4], [5, 2]])
test[0][1] # array([5, 2])
test[1,1,1] # 9
test[0, 0, 1] = 10 # 4 -> 10
test # array([[[ 1, 10], [ 5, 2]], [[ 2, 1], [ 4, 9]]])
- 슬라이싱(slicing) : 인덱스를 사용해 리스트 일부를 반환
test = np.array( [[1, 4, 5, 2],
[2, 1, 4, 9]])
test[:,3:] # array([[2], [9]]), 전체 행의 3열 이상 출력
test[1,:2] # array([2, 1]), 1행의 1열까지 출력
test[1:4] # array([[2, 1, 4, 9]]), 1 ~ 4행의 모든 열로 1행을 초과하는 인덱스는 무시
- 증가값(step) : 리스트에서 증가값만큼 건너뛰면서 반환, [시작:종료:증가값] 형태로 지원
x = np.array(range(9), int).reshape(3, -1) # 0에서 8까지 정수형의 2차원 데이터 배열을 만듬
x # array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
x[:,::2] # array([[0, 2], [3, 5], [6, 8]])
x[::2,::2] # array([[0, 2], [6, 8]]), 행/열 모두 적용
- arange : range처럼 차례대로 값을 생성, 증가값에 실수형 입력 가능해 소수점 값 주기적으로 생성 가능
- range는 range iterator 자료형을 반환하지만, np.arange 메소드는 numpy array 자료형을 반환
np.arange(5) # array([0, 1, 2, 3, 4])
np.arange(-3, 3) # array([-3, -2, -1, 0, 1, 2])
np.arange(0, 3 ,0.5) # array([0. , 0.5, 1. , 1.5, 2. , 2.5])
- ones : 1로만 구성된 넘파이 배열 생성, shape 크기만큼 메모리 할당하고 1로 채움
# dtype 기본 값 float64, dtype을 지정해 데이터 타입 설정
np.ones(shape=(2, 2), dtype=np.int8) # array([[1, 1], [1, 1]], dtype=int8)
- zeros : 0으로만 구성된 넘파이 배열 생성, shape 크기만큼 메모리 할당하고 0으로 채움
np.zeros(shape=(2,2)) # array([[0., 0.], [0., 0.]])
- empty : 활용 가능한 메모리 공간을 확보해 반환, 메모리 초기화되지 않아 다른 값을 반환
np.empty(shape=(2,2), dtype=np.float32)
# array([[1.5485638e+23, 7.0345183e-43], [0.0000000e+00, 0.0000000e+00]], dtype=float32)
- ones_like : 기존 넘파이 배열과 같은 크기로 만들어 1로 채움
test = np.array(range(6), int).reshape(2, -1)
test # array([[0, 1, 2], [3, 4, 5]])
np.ones_like(test) # array([[1, 1, 1], [1, 1, 1]])
- zeros_like : 기존 넘파이 배열과 같은 크기로 만들어 0로 채움
np.zeros_like(test) # array([[0, 0, 0], [0, 0, 0]])
- empty_like : 기존 넘파이 배열과 같은 크기로 만들 빈 공간으로 채움
np.empty_like(test) # array([[0, 0, -1355869600], [407, 0, -2147483648]])
- identity : 정방 단위 행렬(i 행렬) 생성
np.identity(n=3, dtype=int)
# array([[1, 0, 0],
# [0, 1, 0],
# [0, 0, 1]])
- eye : NxM의 단위 행렬 생성, k값은 k열을 기준으로 단위 행렬 생성(기본값 0)
np.eye(N=3, M=5)
# array([[1., 0., 0., 0., 0.],
# [0., 1., 0., 0., 0.],
# [0., 0., 1., 0., 0.]])
np.eye(N=3, M=5, k=1)
# array([[0., 1., 0., 0., 0.],
# [0., 0., 1., 0., 0.],
# [0., 0., 0., 1., 0.]])
- diag : 행렬의 대각 성분 값 추출
np.diag(np.identity(n=3, dtype=int)) # array([1, 1, 1])
- random : 난수를 생성
- uniform : 균등분포로 값을 생성
- 균등분포 : 주어진 구간 내 모든 점에 대해 나오는 값이 나올 확률이 일정한 분포
# np.random.uniform(시작값, 끝값, 데이터 개수)
np.random.uniform(0, 5, 10)
# array([3.22209946, 2.74944536, 0.346364 , 2.855224 , 2.28926904,
# 2.28470757, 4.89144377, 4.53477816, 2.86051157, 1.20318974])
- normal : 정규분포로 값을 생성
- 정규분포 : 구간별로 확률을 가지는 분포로 평균에 가까울수록 확률이 높다.
# np.random.normal(평균값, 분산, 데이터 개수)
np.random.normal(0, 2, 10)
# array([ 2.52354633, 0.71553675, 0.54250824, -0.75052835, -1.67623756,
# 0.22282107, 0.53414941, 1.90262839, -0.44088655, -1.21667551])
넘파이 배열 연산
- sum : 넘파이 배열 요소의 합을 반환
- axis : 축을 나타내며, 차원이 늘어날 때마다 다룰 수 있는 축의 값이 증가
import numpy as np
test = np.arange(1, 11) # 1에서 10까지의 넘파이 배열 생성
test.sum() # 55
test = test.reshape(2, 5)
test
# array([[ 1, 2, 3, 4, 5],
# [ 6, 7, 8, 9, 10]])
test.sum(axis=0) # array([ 7, 9, 11, 13, 15]), 행끼리 계산
test.sum(axis=1) # array([15, 40]), 열끼리 계산
test = np.arange(1, 13).reshape(3, 4)
third_order_tensor = np.array([test ,test, test])
third_order_tensor
# array([[[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]],
# [[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]],
# [[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]]])
third_order_tensor.sum(axis=0)
# array([[ 3, 6, 9, 12],
# [15, 18, 21, 24],
# [27, 30, 33, 36]])
third_order_tensor.sum(axis=1)
# array([[15, 18, 21, 24],
# [15, 18, 21, 24],
# [15, 18, 21, 24]])
third_order_tensor.sum(axis=2)
# array([[10, 26, 42],
# [10, 26, 42],
# [10, 26, 42]])
- mean : 넘파이 배열 요소의 평균을 반환
test = np.arange(1, 13).reshape(3, 4)
test
# array([[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]])
test.mean(axis=1) # array([ 2.5, 6.5, 10.5])
- std : 넘파이 배열 전체에 대한 표준편차를 반환
test.std() # 3.452052529534663
test.std(axis=1) # array([1.11803399, 1.11803399, 1.11803399])
- np.sqrt : 넘파이 배열 각 요소에 제곱근 연산 수행
test
# array([[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12]])
np.sqrt(test)
# array([[1. , 1.41421356, 1.73205081, 2. ],
# [2.23606798, 2.44948974, 2.64575131, 2.82842712],
# [3. , 3.16227766, 3.31662479, 3.46410162]])
- vstack : 배열을 수직으로 붙여 하나의 행렬 생성
- hstack : 배열을 수평으로 붙여 하나의 행렬 생성
test1 = np.array([1, 2, 3])
test2 = np.array([4, 5, 6])
np.vstack((test1, test2))
# array([[1, 2, 3],
# [4, 5, 6]])
np.hstack((v1,v2)) # array([1, 2, 3, 4, 5, 6])
- concatenate : 축을 고려해 두개의 배열 결합
test1 = np.array([1, 2, 3, 4]).reshape(2,2)
test2 = np.array([[5, 6]]).T # ndarray.T 객체 전치행렬, 1차원은 그대로 1차원
test1
# array([[1, 2],
# [3, 4]])
test2
# array([[5],
# [6]])
np.concatenate((test1, test2), axis=1) # 축 1을 기준으로 결합
# array([[1, 2, 5],
# [3, 4, 6]])
- 사칙연산 : 행렬과 행렬 / 벡터와 벡터 간 사칙연산
test = np.arange(1, 4)
test # array([1, 2, 3])
test + test # array([2, 4, 6])
test - test # array([0, 0, 0])
test / test # array([1., 1., 1.])
test ** test # array([ 1, 4, 27])
- 배열 간의 곱셈은 벡터의 내적 연산으로 이루어진다.
- dot : 두개의 행렬 내적 연산
test = np.arange(1, 10).reshape(3,3)
test
# array([[1, 2, 3],
# [4, 5, 6],
# [7, 8, 9]])
test + 10
# array([[11, 12, 13],
# [14, 15, 16],
# [17, 18, 19]])
- 브로드캐스팅 연산 : 하나의 행렬과 스칼라 값 간의 연산 또는 행렬과 벡터 간의 연산
test1 = np.arange(1, 7).reshape(2,3)
test2 = np.arange(1, 7).reshape(3,2)
test1
# array([[1, 2, 3],
# [4, 5, 6]])
test2
# array([[1, 2],
# [3, 4],
# [5, 6]])
test1.dot(test2) # 2x3 행렬과 3x2행렬의 연산 결과는 2x2행렬이 나온다.
# array([[22, 28],
# [49, 64]])
x = np.arange(1, 10).reshape(3,3)
v = np.arange(10, 20, 30)
x + v
# array([[11, 12, 13],
# [14, 15, 16],
# [17, 18, 19]])
- 비교 연산 : Boolean 배열로 추출
- all : and 조건을 적용해 모두 참일 경우 True
- any : or 조건을 적용해 내부의 값 중 하나라도 참일 경우 True
- np.where : 참인 값들의 인덱스를 반환, 참/거짓에 따라 값으로 지정할 수도 있다.
x = np.array([4, 3, 2])
x > 3 # array([True, False, False])
y = np.array([2, 5, 1])
x > y # array([True, False, True])
(x > 3).all() # False
(x > 3).any() # True
np.where(x > 3) # (array([0], dtype=int64),)
np.where(x > 3, 1, 0) # array([1, 0, 0]), 참/거짓 대신 1/0으로 반환
- np.argsort : 배열 내 작은 순서대로 인덱스 반환
- np.argmax : 배열 내 가장 큰 값의 인덱스 반환
- np.argmin : 배열 내 가장 작은 값의 인덱스 반환
x = np.array([4, 3, 2])
np.argsort(x) # array([2, 1, 0], dtype=int64)
np.argmax(x) # 0
np.argmin(x) # 2
- Boolean Index : 넘파이 배열에 특정 조건의 값들을 추출
x = np.array([4, 3, 2])
y = x > 2
x[y] # array([4, 3])
- Fancy Index : 넘파이 배열에 정수형의 인덱스 위치값들을 추출, 2차원 이상에서도 사용 가능
x = np.array([4, 3, 2])
y = np.array([2, 1, 0])
x[y] # array([2, 3, 4])
- %timeit를 통해 함수의 실행 시간에 대한 평균과 표준편차를 출력
연습문제
데이터 과학을 위한 파이썬 머신러닝 3장 연습문제 풀이
참고문헌
최성철, 『데이터 과학을 위한 파이썬 머신러닝』, 초판, 한빛아카데미, 2022