랜선 자르기
- 시간 제한 : 2 초
- 메모리 제한 : 128 MB
알고리즘 분류
- 이분 탐색
- 매개 변수 탐색
문제
박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다.
이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다. 박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다. 예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)
편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며, 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다고 가정하자. 그리고 자를 때는 항상 센티미터 단위로 정수길이만큼 자른다고 가정하자. N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다. 이때 만들 수 있는 최대 랜선의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그 후 K줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 센티미터 단위의 정수로 입력된다. 랜선의 길이는 231-1보다 작거나 같은 자연수이다.
출력
첫째 줄에 N개를 만들 수 있는 랜선의 최대 길이를 센티미터 단위의 정수로 출력한다.
풀이
이진 탐색을 응용한 매개 변수 탐색 방식을 이용해야 풀 수 있는 문제이다. 나도 해당 개념을 공부해보고 아래와 같이 풀이를 진행해보았다.
- 이진 탐색(Binary Search) : 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법
- 시작점, 끝점, 중간점을 이용해 탐색 범위를 설정해서 플어감
- 매개 변수 탐색(Parametric Search) : 최적화 문제를 결정 문제로 바꾸어 풀 수 있게 해주는 이분 탐색의 응용 방식
최적화 문제 : 어떠한 함수에서 최적의 값을 구하는 문제 풀이
결정 문제 : 답이 예-아니오로 결정된 상태에서 구하는 문제 풀이
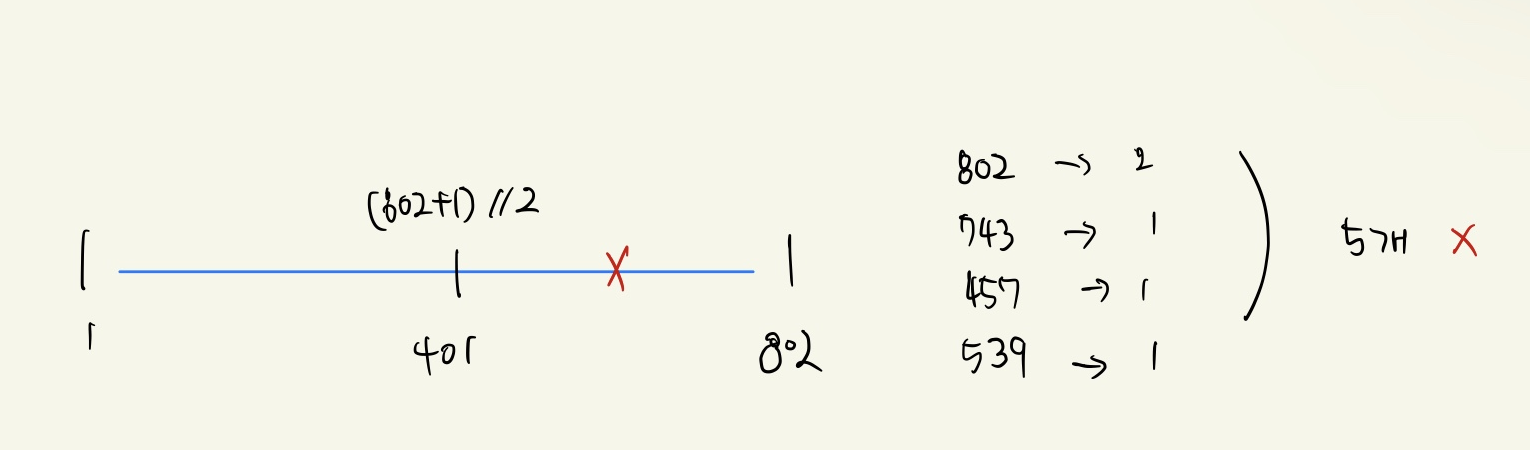예제에서 K=4, N=11 / 802, 743, 457, 539로 입력받을 경우 시작점을 1로 하고 끝점을 802로 하여 (시작점 + 끝점) // 2인 중간점은 401이다. 401로 랜선을 자르면 총 5개의 랜선을 만들 수 있으며, N보다 작으므로 끝점을 401 - 1로 한다. 중간점 401이상의 숫자로는 랜선을 11개로 만들 수 없기 때문이다.
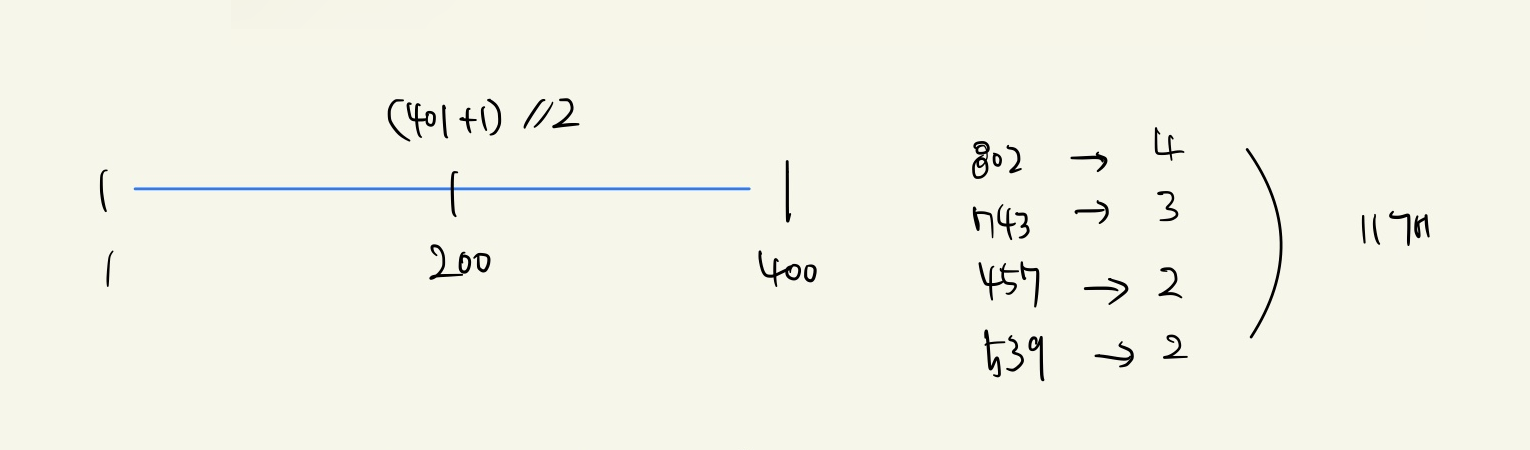시작점을 1로 하고 끝점을 400로 하여 (시작점 + 끝점) // 2인 중간점은 200이다. 200로 랜선을 자르면 총 11개의 랜선을 만들 수 있다. 예제 출력 답이 200이긴 하지만, 문제 풀이 단계에서는 201에서 400까지 숫자들 또한 해당될 수 있기 때문에 시작점을 200 + 1로 하여 과정을 계속 진행한다.
최종적으로 시작점(201) > 끝점(200)이 되면 끝점을 랜선의 최대 길이로 제출하면 된다.
소스 코드
Python
K, N = map(int, input().split())
array = []
for i in range(K):
array.append(int(input()))
minNum = 1
maxNum = max(array)
while minNum <= maxNum:
sum = 0
midNum = (minNum + maxNum) // 2
for i in array:
sum += i // midNum
if N <= sum:
minNum = midNum + 1
else:
maxNum = midNum - 1
print(maxNum)
Ghost