체스판 다시 칠하기
- 시간 제한 : 2초
- 메모리 제한 : 128MB
알고리즘 분류
- 브루트포스 알고리즘
문제
정사각형으로 나누어져 있는 M×N 크기의 보드를 잘라서 8×8 크기의 체스판으로 만들려고 한다.
체스판은 검은색과 흰색이 번갈아서 칠해져 있어야 한다. 구체적으로, 각 칸이 검은색과 흰색 중 하나로 색칠되어 있고, 변을 공유하는 두 개의 사각형은 다른 색으로 칠해져 있어야 한다. 따라서 이 정의를 따르면 체스판을 색칠하는 경우는 두 가지뿐이다. 하나는 맨 왼쪽 위 칸이 흰색인 경우, 하나는 검은색인 경우이다.
8 X 8 크기는 아무데서나 골라도 되며, 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 M이 주어진다. N과 M은 8보다 크거나 같고, 50보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어진다. B는 검은색이며, W는 흰색이다.
출력
첫째 줄에 지민이가 다시 칠해야 하는 정사각형 개수의 최솟값을 출력한다.
풀이
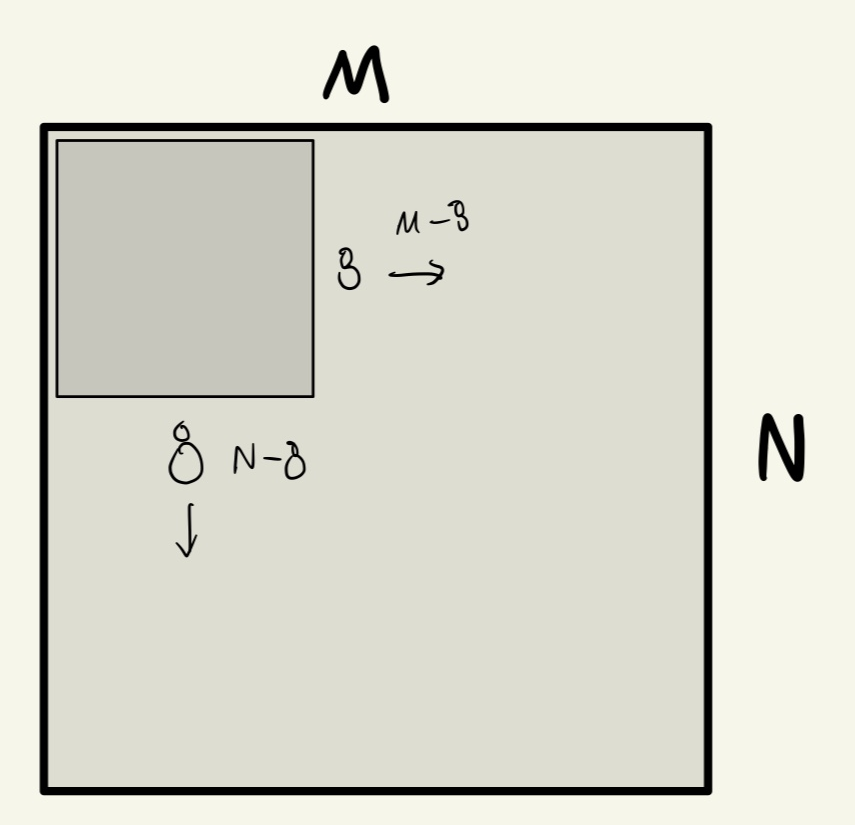브루트포스 알고리즘을 이용하면 되므로, 가능한 모든 경우의 수를 탐색한다.
N - 8 * M - 8만큼 8 * 8의 체스판을 이동하면서 64개의 칠해야하는 체스 칸을 체크하면 된다.
소스 코드
Python
# 1018번 체스판 다시 칠하기
N, M = map(int, input().split())
row = ["BWBWBWBW", "WBWBWBWB"]
board = []
color = 2500
for i in range(N):
board.append(input())
for i in range(N - 7):
for j in range(M - 7):
for c in range(2):
temp = 0
for a in range(i, i + 8):
for b in range(j, j + 8):
if c == 0:
row.sort()
else:
row.sort(reverse=True)
if row[a % 2][b % 2] != board[a][b]:
temp += 1
if color > temp:
color = temp
print(color)
Ghost